Nu er det tid til et indlæg i kategorien “Syntesen”. Denne gang er indlægget målrettet de, der er primært tænker rationelt og i analyser. Formidlingen sker igennem en opgave, der kræver matematiske færdigheder kombineret med balanceret brug af højre og venstre hjernehalvdel, men som også på en smuk måde formidler treenigheden i syntesen.
Den originale udgave af opgaven kommer fra Ned Hermann, der er ophavsmand til Whole Brain Thinking og HBDI. Lasse Zäll fra Stifinderprogrammet, har på et tidspunkt stillet opgaven på Facebook. Her poppede den tilfældigvis op for mig i min nyhedsstrøm, selvom det var 3 år siden han havde lagt den op. Når du læser opgaven her, er det i en omskrevet form, fra den oprindelige. Måden at løse den på, er dog den samme.
Som det fremgår af min HBDI profil, får jeg en stærk præference for analytisk tænkning, når jeg er under pres. Det var lige præcis i sådan en situation jeg arbejdede med opgaven. Det virkede lidt som terapi på mig, om end jeg kæmpede unødigt meget med opgaven.
Opgaven
Langt oppe i Norge er en flok biler på vej på skiferie. Vejret viser sig fra en uheldig side, og har nødvendiggjort snerydning. Mængden af biler bag sneploven har efterhånden gjort at køen er 2 kilometer lang, uden mulighed for at overhale. I dette tidspunkt ankommer en bil fra det norske vejdirektorat. Forhold længere fremme på sneplovens rute har gjort, at den skal ændre retning i forhold til den oprindelige plan. Sneploven er dog ikke kontaktbar, og da det er umuligt at overhale, kan beskeden ikke leveres i bil. Det vidste de godt fra vejdirektoratet, og derfor har de medbragt et kort over den nye rute til chaufføren i sneploven, og planlagt at sneploven skal indhentes til fods af en budbringer, som er passager i bilen. Køen bevæger sig med en konstant hastighed. Budbringeren forlader bilen, indhenter sneploven til fods, afleverer beskeden og returnerer til bilen. Da budbringeren vender tilbage, er bilen på præcis det sted, hvor sneploven var, da budbringerens rejse begyndte. Føreren af bilen synes budbringeren var lidt langsom til at levere beskeden, så de kommer til at diskutere hvilken distance budbringeren har tilbagelagt.
Det er her du kommer ind i billedet. Du skal ud fra de foreliggende oplysninger hjælpe de to personer i bilen med at fastlægge distancen, som budbringeren har tilbagelagt. For nemhedens skyld kan du antage at budbringeren har rejst med en konstant hastighed, at køen har gjort det samme, og at afleveringen af kortet ikke tog nævneværdig tid. God fornøjelse…
Læs ikke videre før du vil have hjælp til at løse opgaven!
At tvivle på løsningen
Når du læser dette er det muligt at du har et svar. Det svar kan enten være rigtigt eller forkert. Derfor gennemgår denne overskrift nogle forskellige bud på svar, som alle er forkerte. Var det et af disse svar du havde i tankerne, har du dermed mulighed for at vende tilbage til opgaven og give den et nyt forsøg.
Mulige forkerte svar kunne være:
- At der ikke er nogen løsning
- At løsningen afhænger af parametre som tid og hastighed, der ikke er oplyst
- At løsningen er 2 kilometer
- At løsningen er 3 kilometer
- At løsningen er 4 kilometer
- At løsningen er 5 kilometer
Ingen af disse svar er rigtige. Var dit svar iblandt, så på den igen!
At forstå opgaven
Når du når hertil har du måske et svar, som du tror er rigtigt, fordi det ikke var blandt de forkerte. Måske vil du bare gerne have noget hjælp til at komme videre, uden at få løsningen med det samme.
Første skridt på vejen mod en løsning er at forstå opgaven præcist. Det handler altså om at få nogen fakta på plads.
Det eneste tal vi har fået oplyst er, at køen er 2 kilometer lang. Vi ved derfor at budbringeren minimum skal rejse 2 kilometer + den afstand sneploven har tilbagelagt i løbet af rejsen. Fordi køen er 2 kilometer lang og hver bil har flyttet sig nøjagtigt 2 kilometer fra budbringeren rejser ud til budbringeren er tilbage, ved vi at der er 4 kilometer mellem udgangspunktet for vejdirektoratets bil ved starten af rejsen, og sneplovens placering ved slutningen. Budbringeren rejser både frem og tilbage, men det kan aldrig blive en rejse på mere end 6 kilometer. Derfor er svaret hverken 2 eller 6 kilometer, men et eller andet sted derimellem.
Er dit svar ikke mellem 2 og 6, kan du nu gå tilbage og forsøge igen.
At visualisere forløbet
Vi har behov for at kunne opstille nogle ligninger med nogle ubekendte, for at kunne løse opgaven. Det kræver dog at man er i stand til at visualisere hændelsesforløbet og uddrage nogle oplysninger herfra.
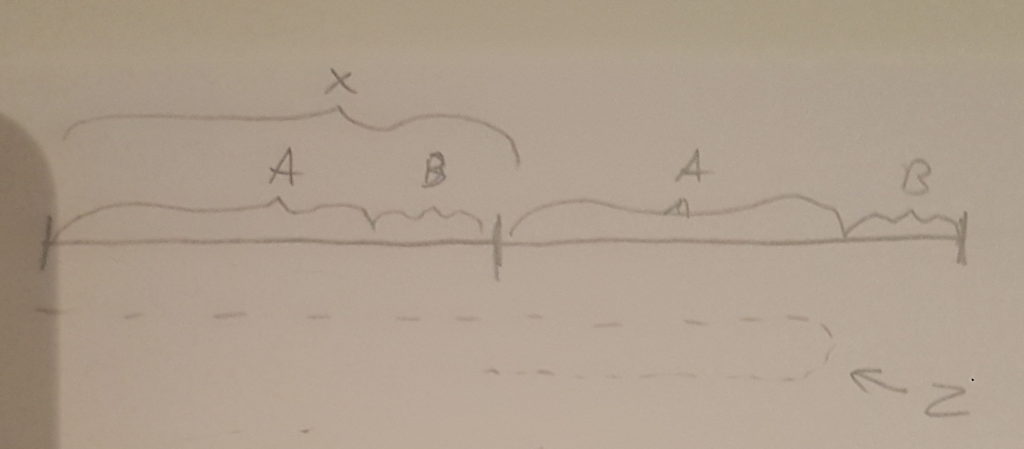
På billedet her er ruten for budbringeren visualiseret. Der er to strækninger på X, og ud fra opgaven er X=2 kilometer. Den stiblede linje kaldet Z er budbringerens rejse.
Den tid der går fra budbringeren starter til sneploven er nået, kan vi kalde T1. På den tid rejser både sneploven og vejdirektoratets bil, A kilometer. På turen ud har budbringeren derfor rejst X + A, dvs. 2 + A kilometer.
Den tid der går fra kortet er afleveret til budbringeren er tilbage kan vi kalde T2. På den tid rejser budbringeren A igen. Denne gang rejser vejdirektoratets bil afstanden B, der også kan beskrives som X – A, dvs. 2 – A.
Budbringerens rejse Z, kan beskrives som X + 2A, og derfor 2 + 2A.
At opstille ligninger
Da jeg forsøgte at løse opgaven foregik det i sengen, hvor jeg ikke havde papir og blyant til rådighed. Det lykkedes mig at komme frem til ligningen Z = X + 2A i hovedet, men at udtrykke Z på en anden måde voldte mig en del kvaler. Før jeg havde gjort forsøget, havde jeg tjekket løsningen, men da jeg ikke fuldstændig forstod løsningen gik jeg i gang med papir og blyant alligevel.
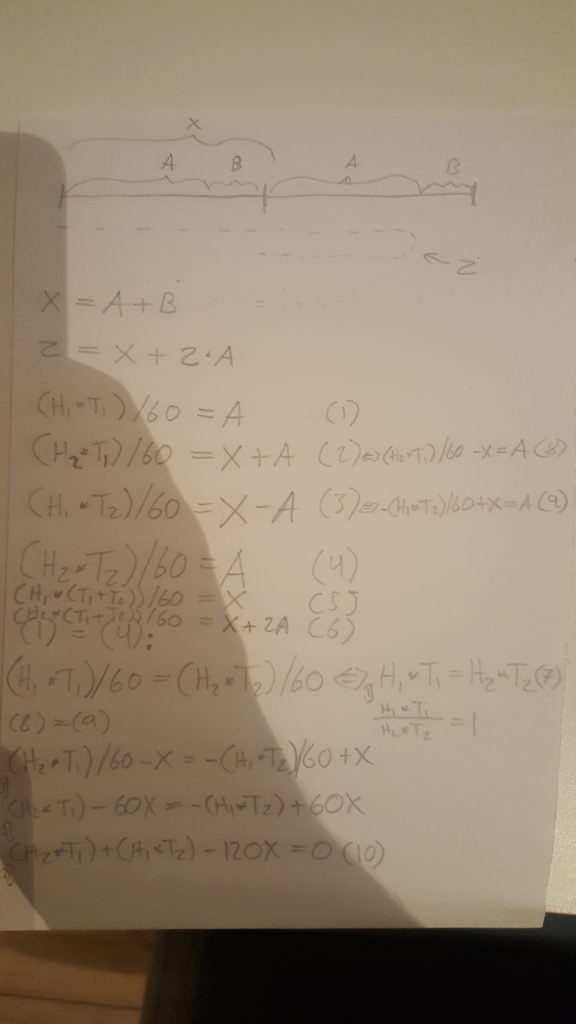
Som du kan se, blev det til en masse ligninger med en masse ubekendte. Ligningerne kommer fra formel for beregning af hastighed, afstand og tid.
H1 er hastigheden på køen, H2 er hastigheden på budbringeren, T1 er tiden for rejsen til sneploven, T2 er tiden for rejsen tilbage.
Det lykkes mig at finde løsningen ved at bruge ligningerne (1), (3) og (5). Min fremgangsmåde var at fastsætte hastigheden på køen (H1) til et arbitrært tal. F.eks. 3 km/t. Derved reducerer jeg disse tre ligninger fra at have 3 ubekendte til kun at have 2.
Skulle du have lyst til at forsøge at løse de her ligninger, kan du gøre forsøget nu. Der er dog en nemmere løsning.
En nemmere måde at løse problemet på
Problemet med den foregående løsning var, at den ikke svarede til den løsning jeg havde set, og ikke kunne forstå. Resultatet var det samme, men metoden var forskellig. Sådan noget har jeg svært ved at acceptere.
Pludselig slog det mig dog, at det var fordi tiden og hastigheden var unødvendige parametre i at løse opgaven. Det hele kunne løses med afstand.
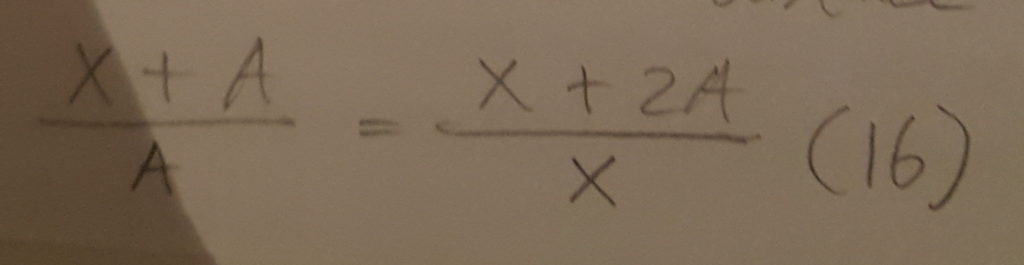
Den venstre side udtrykker rejsen i første tidsrum T1. Her rejser budbringeren X + A, mens sneploven og dermed køen kun rejser A. Resultatet er et udtryk for deres hastighedsforskel.
Deres hastighedsforskel er ens på forskellige tidspunkter, så ved at udtrykke den afstand de har rejst i forhold til hinanden på en anden måde, får vi mulighed for at opstille en ligning.
Den højre side udtrykker den samlede rejse, dvs. T1 + T2. Her rejser budbringeren som beskrevet tidligere X + 2A. I samme tidsrum rejser hele køen X. Da vi kender X får vi en situation, hvor vi kun har én ubekendt, nemlig A.
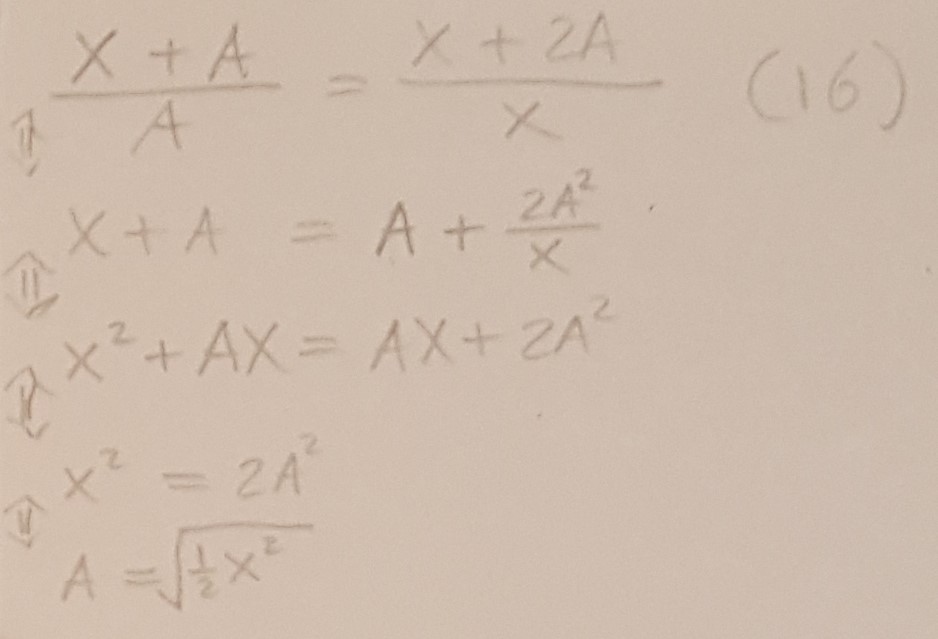
Herved bliver A kvadratroden af 0,5 * 2^2, eller dvs. kvadratroden af 2.
Nu kan vi udregne Z = X + 2A => Z= 2 + 2 * 2^0,5, som giver 4,8284 km.
Det er den distance budbringeren har rejst for at nå frem til sneploven og tilbage til bilen.
Opgaven som eksempel på treenigheden i syntesen
Syntesen består som et træ af både højdevækst og tykkelsesvækst. Højdevæksten er beskrevet som treenigheden, tykkelsesvæksten er en balance mellem modsætninger. Mit første forsøg på at beskrive det, var i indlægget om mit nye logo. Fra dette indlæg vil jeg gerne gentage et citat af Charles Sanders Peirce:
We have seen that the conception of the absolute first eludes every attempt to grasp it; and so in another sense does that of the absolute second; but there is no absolute third, for the third is of its own nature relative, and this is what we are always thinking, even when we aim at the first or second. The starting-point of the universe, God the Creator, is the Absolute First; the terminus of the universe, God completely revealed, is the Absolute Second; every state of the universe at a measurable point of time is the third.
I opgaven har vi et “første”. Det er selve situationen i Norge som den udspiller sig. Vi også et “andet” de faktiske omstændigheder omkring det der har udspillet sig. Det “tredje” er selve vores løsning af opgaven.
Vi kan ikke erkende situationen fuldt ud, det vil aldrig være muligt. Det vil sige, at selvom vi sigter efter “første” eller “andet” har vi kun det tredje. Peirce beskriver også det “tredje” som vores bevidsthed, og ved hjælp af matematikken bliver vi bevidste om afstanden (underlagt nogen forudsætninger).
Vores resultat er relativt præcist. Det er ikke en gengivelse af virkeligheden, men det er en gengivelse der er præcis nok til at vi kan bruge den til at navigere efter.
Vi ved stadig ikke hvor hurtigt køen rejste, eller hvor hurtigt budbringeren rejste, ej heller hvor lang tid hele forløbet tog. De sandheder har vi ingen forudsætninger for at erkende med de oplysninger vi har fået.
I min metafor af treenigheden som et træ, er rødderne selve situationen, kronen er de faktiske omstændigheder, og stammen – som forbinder dem – er det rationelle matematiske arbejde, der lader os opnå en relativ sandhed om den uerkendelige absolutte sandhed.
