Forleden fik jeg lagt bogen “The haystack syndrome” op på bloggen. Det er en fantastisk bog, og den mindede mig om 3 seancer, hvor jeg underviste i produktionsstyring på cand.merc. i styring og ledelse på SDU i Kolding. Her anvendte jeg et eksempel fra bogen, som du nu kan få lov til at prøve kræfter med!
Goldratt, der har skrevet bogen, bygger op til eksemplet ved at spørge, om det er muligt at svare på spørgsmålet: “Hvad bliver virksomhedens profit i næste kvartal?” altså ikke bare som et estimat, men som et kvalificeret svar, med en præcision der kan måles i decimaler.
Han svarer selv, at den typiske reaktion vil være, at der er for mange usikkerheder. Der er usikkerheder relateret til:
- Kunderne
- Leverandørerne
- Virksomhedens egne processer
- Maskinparken
- Arbejdskraften
- Ledelsen
Herefter konkluderer han spydigt, at sådanne svar mest af alt lyder som en liste med undskyldninger. Derfor designer han eksemplet her, som den perfekte fabrik, hvor de her problemer ikke er til stede og alt usikkerhed dermed er elimineret.
- Virksomheden sælger og producerer bare to produkter, P og Q.
- Arbejdskraften er ekstremt veltrænet og pålidelig, den tid de forskellige processer tager er kendt, og fejlraten er 0%. Ingen variation i kvaliteten.
- Prisen er fast for begge produkter. P koster 90 pr. stk og Q koster 100 pr. stk.
- I modsætning til virkeligheden er efterspørgslen kendt. Markedet efterspørger ugentligt 100 stk. P og 50 stk. Q. Det vil sige, at det her antal er hvad markedet rent faktisk vil aftage, hvis virksomheden producerer det.
- P består af 2 råmaterialer (RM1 og RM2), samt en underkomponent der købes ude i byen (PP). RM1 og RM2 koster begge 20 pr. enhed, og PP koster 5.
- Q består af 2 råmaterialer (RM2 – samme som P og RM3), RM2 og RM3 koster begge 20.
- Der er 4 medarbejdere: A, B, C og D. Hver medarbejder har to funktioner, og der er ingen omstillingstid mellem funktionerne. Til gengæld kan de ikke udføre hinandens arbejde. A kan ikke lave B, eller nogen af de andres arbejde.
Hver medarbejder er til rådighed 5 dage om ugen i 8 timer pr. dag. Dvs. 2.400 minutter pr. medarbejder pr. uge. - Virksomhedens driftsomkostninger er 6.000 pr. uge. Heri er indeholdt alle ikke-variable omkostninger, såsom lønnen til de fire medarbejdere, og alt andet. Det eneste der ikke er indeholdt er prisen på RM1, RM2, RM3 og PP.
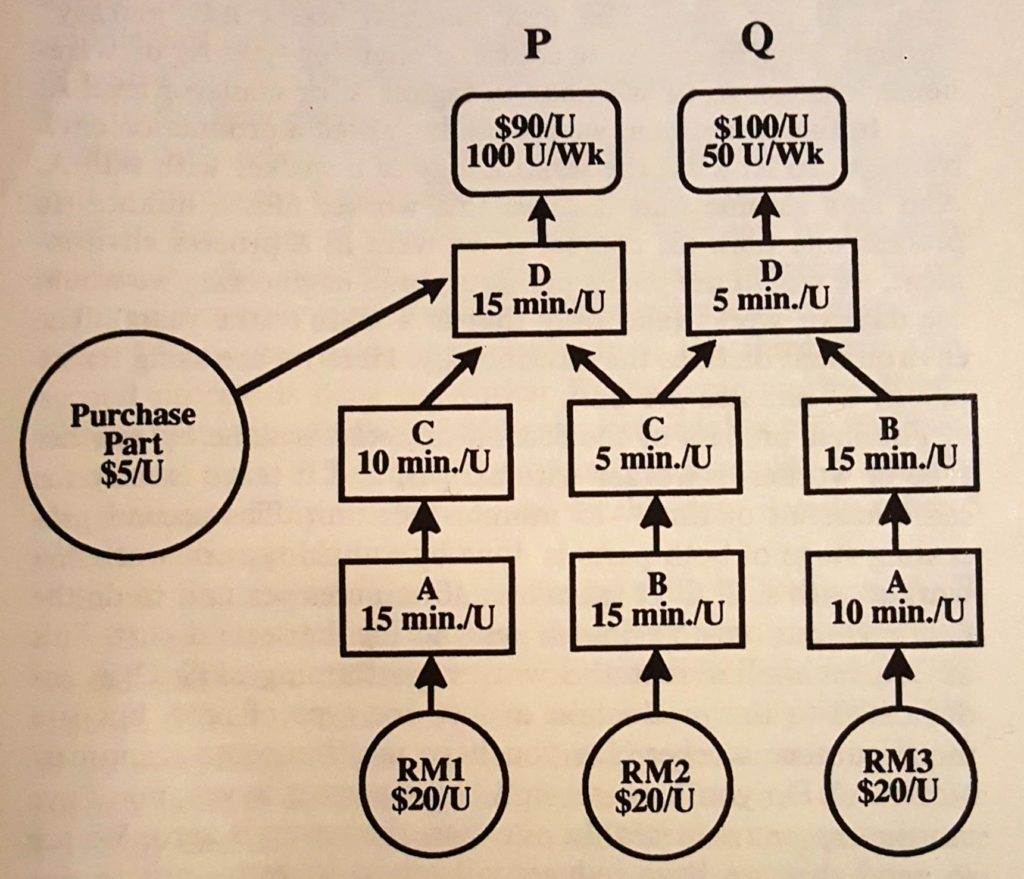
- For nemhedens skyld er der en oversigt over flowet nedenfor.
Bemærk at P og Q består af en fælles komponent.
Hvis man skal producere én P skal der bruges 1 stk. PP, 1 stk. RM1 bearbejdet af A og C, samt 1 stk. RM2 bearbejdet af B og C, som til sidst samles af D.
Hvis man skal producere én Q skal der bruges 1 stk. RM2 bearbejdet af B og C, samt 1 stk. RM3 bearbejdet af A og B, som til sidst samles af D.
I diagrammet nedenfor er bearbejdningen af RM2 vist samlet for at spare plads, der er altså ikke krav om at P og Q produceres samtidigt.
Det her er en virksomhed med perfekt information, så nu er det måske muligt at svare på det indledende spørgsmål (med en lidt anden tidsperiode):
Hvad er den største profit (eller det mindste tab), den her virksomhed kan præstere pr. uge?
Nu er det tid til at svare på spørgsmålet, og jeg anbefaler at du regner på det før du går videre.
Her er med vilje nogle tomme linjer, så du ikke fristes til at se svaret med det samme.
Gå ikke videre før du har et bud!
Jeg mener det! Der er en chance for at du kan lære noget her!
På det tidspunkt Goldratt skrev bogen, skulle han eftersigende have præsenteret regnestykket for 10.000 ledere. Erfaringen var at kun 1% af dem kunne give det rigtige svar. Du skal derfor ikke være alt for ked af det, hvis det glipper for dig.
En af de typiske svar er at det maksimale overskud er 1.500 pr. uge. Det opstår på en eller anden måde som en antagelse om, at det er efterspørgslen, der sætter grænsen for produktionen.
Det kan f.eks. være at man gør tiden op, og konstaterer at det tager 60 minutter at lave P og 50 minutter at lave Q. Det er 6.000 minutter for efterspørgslen efter P og 2.500 minutter for efterspørgslen efter Q. Produktionen af den samlede efterspørgsel tager altså 8.500 minutter, og der er 4 medarbejdere med 2.400 minutter til rådighed, dvs. 9.600 en kapacitetsudnyttelse ca. 89%.
Derved bliver resultatet: 100 x (90 – 45) + 50 x (100 – 40) – 6000 = 1.500
Regnestykket er rigtigt under antagelsen om at markedet er begrænsningen, men antagelsen er forkert og derfor er resultatet det også!
Var 1.500 dit bud? Prøv igen, inden du scroller videre.
Ok, vi går videre. Vi leder efter en begrænsning inde i virksomheden, lad os se på hvor meget der er behov for hver enkel ressource.
A: 100P x 15 min + 50Q x 10 min = 2.000 min (2.400 min til rådighed)
B: 100P x 15 min + 50Q x (15 + 15) min = 3.000 min (2.400 min til rådighed)
C: 100P x (10 + 5) min + 50Q x 5 min = 1.750 min (2.400 min til rådighed)
D: 100P x 15 min + 50Q x 5 min = 1.750 min (2.400 min til rådighed)
Vi kan se vi har et problem med medarbejder B. 100P og 50Q medfører et behov for medarbejder B i 3.000 minutter, men medarbejderen er kun til rådighed i 2.400 minutter, og der er ikke noget vi kan gøre for at få mere af B.
Hvad gør vi så? Vi må nødvendigvis beslutte hvilket produkt, der er bedst at producere. Det ligner en no-brainer.
Hvilket produkt har den korteste produktionstid? Q
Hvilket produkt har den højeste salgspris? Q
Hvilket produkt har det højeste dækningsbidrag? Q
Hvilket produkt har den højeste dækningsgrad? Q
Så vi producterer Q først, og så producerer vi P med det der er tilbage.
Alle 50Q kan produceres, og de optager medarbejder B i 1.500 minutter.
Det efterlader 900 minutter til at producere P, så dem kan vi lave 60 stk. af!
Derved bliver resultatet: 60 x (90 – 45) + 50 x (100 – 40) – 6000 = -300
UPS! I stedet for 1.500 i profit bliver det 300 i tab! Av…
Regnestykket bygger på antagelsen om at Q er det bedste produkt at producere, men antagelsen er forkert, og derfor er resultatet det også!
Men hvad gør vi så, skal vi så producere P først, eller skal vi have et mix af de to? Du har nu chancen for at regne igen, hvis det her var dit svar.
Okay, nu kan der snart ikke koges mere suppe på det her eksempel. I det her afsnit kommer det rigtige svar, og det argument, der leder frem til svaret. Men først vil jeg nævne, at selvom dit resultat ikke har passet med de to foregående, er du ikke home-safe endnu!
De tre gange jeg har præsenteret eksemplet for cand.merc. studerende (der allerede havde en bachelorgrad i økonomi!), har jeg set mange vilde eksempler på hvordan regnestykket kan laves forkert. Det skyldes ofte, at man er hoppet ud i nogen vilde omkostningsallokeringer, som ikke gør andet end at forstyrre klarheden i eksemplet, og medfører en falsk tryghed om at man har styr på det, fordi det er kompliceret.
Svaret på opgaven er meget simpelt. Vi har for lidt tid hos medarbejder B, så den medarbejder er bestemmende for, hvad vi skal producere!
Det tager B 30 minutter at lave Q, men kun 15 minutter at lave P. For hvert minut B laver Q bidrager det med 2 på bundlinjen (60 i dækningsbidrag divideret med 30 minutter). Når B laver P bidrager det med 3 på bundlinjen (45 i dækningsbidrag divideret med 15 minutter).
Virksomheden skal altså lave så meget P som markedet efterspørger, og derefter fylde op med Q. P tager 1.500 minutter af B’s tid, og det efterlader 900 minutter til at lave Q, som dem kan vi lave 30 stk. af.
Derved bliver resultatet: 100 x (90 – 45) + 30 x (100 – 40) – 6000 = 300
300 i profit pr. uge! Det er det rigtige svar!
Var dit svar noget andet end 300? Så er der en risiko for at du har gjort regnestykket mere kompliceret end de data du blev forelagt krævede. Er der en risiko for at du kunne begå samme fejl, når data ikke er perfekte som i dette eksempel?
Måske… men så kan du glæde dig over, at en fejl er sværere for andre at opdage, når der er mange andre faktorer, der kan få skylden. Hvis det altså er nogen trøst. 🙂