Kender du “The Nine Dot Puzzle”? En opgave der udfordrer dig til at tænke ud af boksen, for at finde løsningen. Jeg beskrev denne opgave tilbage i 2007, i et indlæg med titlen “Dine rammer om verden“. Siden er jeg blevet klogere på opgaven, og derfor giver det mening at genbesøge den.
Som det fremgår af det gamle indlæg, lærte jeg første gang opgaven at kende i min barndom. Min søster præsenterede den for mig. På det tidspunkt kunne jeg ikke løse den, og mente hun havde givet mig falske forudsætninger.
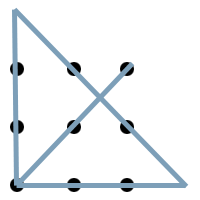
Opgaven er ganske simpel: Forbind alle 9 prikker med højst 4 lige streger, uden at løfte skriveredskabet fra papiret (At køre tilbage af samme streg betragtes som en ny streg).
Hvis du gerne vil prøve kræfter med opgaven, foreslår jeg at du printer billedet ovenfor eller selv tegner prikkerne på et stykke papir og forsøger nu.
Oprindeligt brugte jeg opgaven til at vise, hvordan vi sætter rammer for vores forståelse. De rammer styrer vores opfattelse, og dermed også vores problemløsning. På daværende tidspunkt var jeg kun bevidst om én løsning på opgaven.
Sidenhen læste jeg en bog om Theory of Constraints tankeprocesser – “Thinking for a change” af Lisa Scheinkopf, og her blev eksemplet foldet ud med yderligere løsninger. I denne periode var jeg PhD-studerende og interesserede mig for hvordan man skiftede ledelsesfilosofi i en virksomhed. Her blev opgaven et godt eksempel på et paradigmeskifte.
Et paradigme opstår nemlig i det øjeblik, at vi fastfryser nogen antagelser om verden, og undlader at stille spørgsmålstegn ved dem. De fastfrosne antagelser begrænser rummet for mulige løsninger på et problem, og giver os et afgrænset felt at undersøge for at finde en løsning.
Den klassiske løsning på Nine Dot Puzzle
Opgaven passede så godt til indlægget om “dine rammer om verden”, fordi mange mennesker har en tilbøjelighed til at tegne en imaginær kasse rundt om prikkerne. Når løsningen skal findes bliver stregerne derfor ikke længere end afstanden mellem de yderste prikker. Det gør det umuligt at finde en løsning på opgaven.
Den klassiske løsning er at bryde denne imaginære boks, og forlænge to af stregerne ud af den imaginære kasse. Det ser sådan her ud:
Løsningen giver ofte anledning til et “aha-øjeblik”. Selvfølgelig var det bare sådan man skulle gøre. Det er jo simpelt! Men, men, men, der er mange flere fastfrosne antagelser, og mange flere løsninger.
De kreative løsninger
Den klassiske løsning er meget analytisk og logisk af natur. Det giver en særlig tilfredshed at finde denne løsning. Det er fordi den klassiske løsning holder sig inden for et særligt paradigme, som vi alle er vokset op med.
Jeg formulerer bevidst reglerne meget simpelt og vælger nogen helt bestemt ord. I stedet for prikker, kunne jeg skrive punkter, og i stedet for streger, kunne jeg skrive linjer.
Inden for geometrien har punkter og linjer ingen masse. Sagt på en anden måde, har ingen af dem noget areal. Disse forudsætninger ligger tungt i sindet på mennesker, der er blevet undervist i matematik. Den klassiske løsning er så tilfredsstillende, uanset om prikker og streger har masse eller ej.
Det ville f.eks. være ret let at høvle siden af en blyant og lave én stor fed streg, hen over alle prikkerne. Sådan kan man ikke gøre med linje, men det er ikke noget problem med en streg.
Hvad med at lave nogen meget lange streger, der rammer toppen af den øverste venstre prik, og bunden af den øverste højre prik, og så vende om når det er muligt at gøre det samme ved den midterste række, og til sidst den nederste? Det er en løsning med tre streger. Den fungerer på prikker, der har masse, men ikke på punkterne.
Og der er endnu flere forudsætninger. De fleste antager, at det er urimeligt at ændre papiret. Med en smule origami er det let at folde papiret så prikkerne står på en helt lige linje, og én enkelt streg kan køre igennem dem alle.
Årsagen til dette indlæg er, at opgaven poppede op for mig i en dialog om “Klein Bottles“, som kun har én side. En anden populær én sidet objekt er Möbiusbåndet. En lidt avanceret løsning er derfor at twiste papiret og tape enderne sammen, så du pludselig har et stykke papir med kun én side. Herved kan du lave én lang streg som rammer alle prikker (Ja, det er ikke nemt at tegne stregen, men det er teoretisk muligt).
Hvordan lader du dig begrænse af dit paradigme?
Det er min erfaring at folk, der skal løse opgaven, falder i fire kategorier:
- De der tvivler på, at der overhovedet findes en løsning på opgaven.
- De der stoler på at løsningen findes, men bliver alt for frustrerede over at stirre sig blind på “kassen”
- De der finder den klassiske løsning og stiller sig tilfreds med at have løst opgaven med 4 streger.
- De der lykkes med at bryde yderligere antagelser og kreativt går i gang med at finde massevis af løsninger.
Prøv at se bort fra den her simple opgave et øjeblik. Ansku i stedet selve livet.
Hvor ofte siger du: “Det kan ikke lade sig gøre!”?
Hvor ofte siger du: “JEG kan ikke løse det her problem!”?
Hvor ofte siger du: “Det problem har jeg allerede løst!”?
Hvor ofte siger du: “Der må være endnu bedre måder at løse det her på!”?
Det er min påstand at de fire kategorier af reaktioner på opgaven relaterer sig til de fire tænkestile i Whole Brain Thinking. Det er også min påstand at alle reaktioner kan være både sunde og usunde i forhold til de udfordringer du møder i dit liv.
Nogen gange er det bedst at lade et problem ligge, fordi det er for besværligt at finde en løsning. Andre gange giver det mening at kende sine styrker, og lade andre tage over. Nogen gange skal man stille sig tilfreds med den bedste af de kendte løsninger. Andre gange skal man blive ved med at søge bedre løsninger, end dem man bliver tilbudt af den gængse forståelse.
Men hvis vi ukritisk brugte den samme reaktion på alle problemer, blev livet pludselig meget fattigt at leve. Reaktionerne bliver uproduktive på hver deres måde. “Det kan ikke laves om!”, “Jeg duer ikke til noget som helst!”, “Det bliver ikke bedre end det her!” og “Det bliver aldrig godt nok!”
Tænk over det, næste gang du møder en svær udfordring!